Background

Derivatives are just the idea of a slope, just at a single point instead of two.

When you were taught slope, you were taught that it was rise over run:

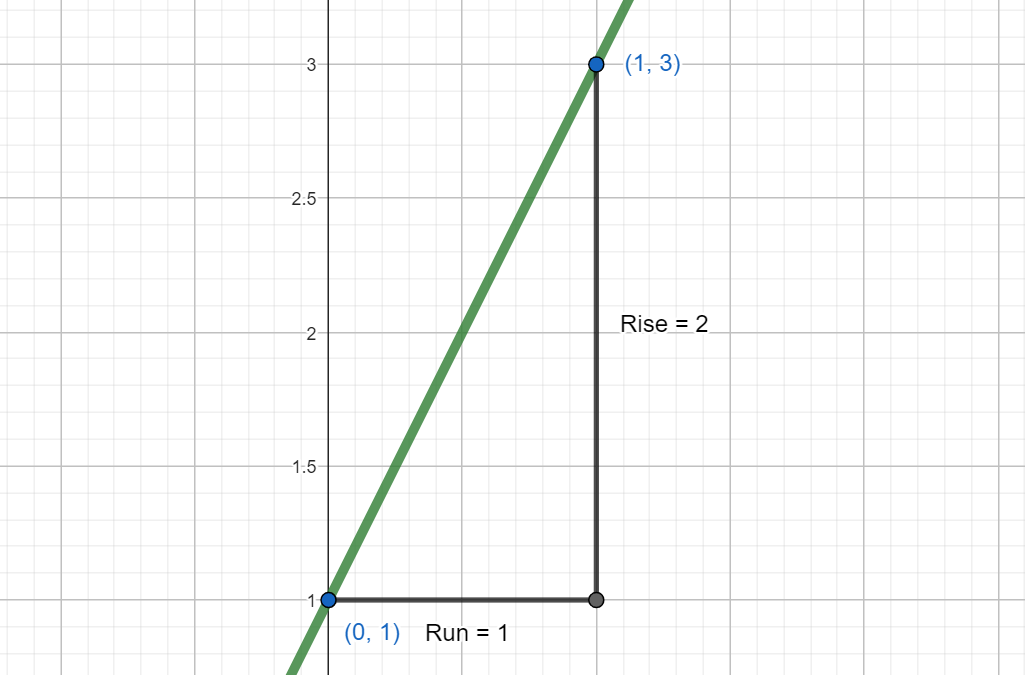
We use this equation to calculate the slope: $$ \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $$

So, our slope is two. At any point on the graph, the slope will still be two.

However, what about for more complicated line, like this quadratic function?

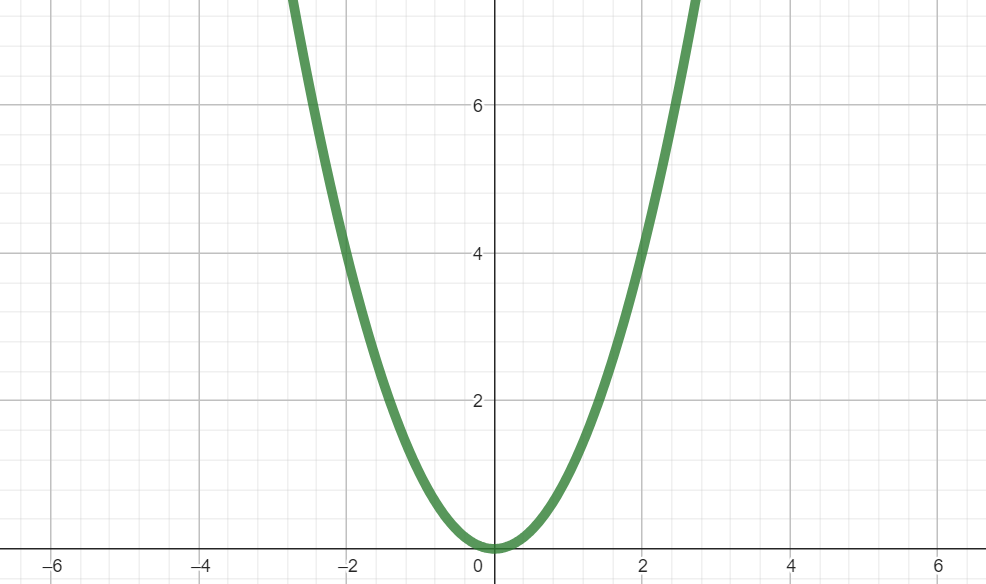
The slope is constantly changing for this function. It wouldn't make sense to find the slope at a single point using our previous equation.

What we can do, however, is bring our two points closer and closer together so that our calculated rate of change is more and more accurate. See how the line gets closer to a slope that better represents that part of the function as we bring the points closer together.

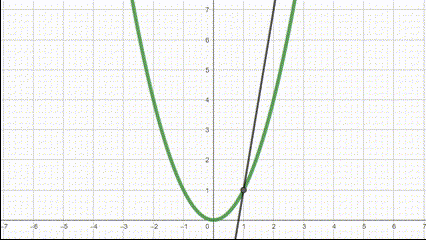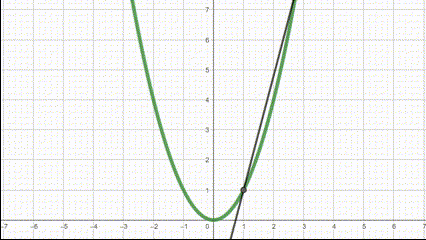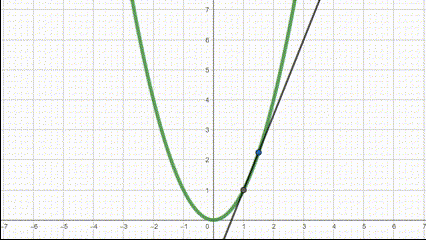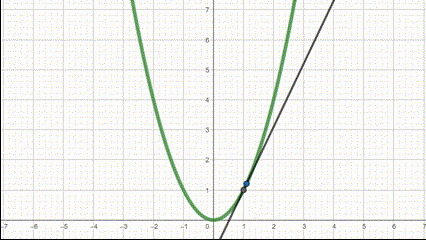
A derivative is just the slope of two points brought so close together, that we can basically just say that they are at a single point. As a result, we can find the slope at one point, rather than two, making a more useful slope for non-linear functions.

Defining a Derivative

Here's how it works:

We define two point on a function $f(x)$, a $\text{Point 1}$ and $\text{Point 2}$. $\text{Point 1}$ has coordinates $(x_{1}, y_{1})$, and $\text{Point 2}$ has coordinates $(x_{2}, y_{2})$. This is the set up that we had before.

$$ \begin{matrix} \text{Point 1}: & (x_{1}, y_{1}) \\ \text{Point 2}: & (x_{2}, y_{2}) \end{matrix} $$

The first thing we do is to replace $y$ with $f(x)$, so that changing $x$ automatically changes $y$ according to our defined function. So, our coordinates are now:

$$ \begin{matrix} \text{Point 1}: & (x_{1}, f(x_{1})) \\ \text{Point 2}: & (x_{2}, f(x_{2})) \end{matrix} $$

The final thing we have to do is to bring the two points close together. We can do this by:

1. defining an incredibly small distance $h$
2. saying that $x_{2}$ is an $h$ distance from $x_{1}$. In other words, $x_{2}=x_{1}+h$

So our coordinates are now:

$$ \begin{matrix} \text{Point 1}: & (x_{1}, f(x_{1})) \\ \text{Point 2}: & (x_{1} + h, f(x_{1} + h)) \end{matrix} $$

Since the only variable we are using is $x_{1}$, we can just write it as $x$. So, our coordinates are:

$$ \begin{matrix} \text{Point 1}: & (x, f(x)) \\ \text{Point 2}: & (x + h, f(x + h)) \end{matrix} $$

Now, we just plug these coordinates into our $y_{2} - y_{1} / x_{2} - x_{1}$

$$ \frac{y_{2} - y_{1}}{x_{2} - x_{1}}=\frac{f(x + h) - f(x)}{x + h - x} =\frac{f(x + h) - f(x)}{h} $$

Previously, we defined $h$ as just a really small change in $x$. We can actually define it in the equation itself using something called a limit:

$$ \boxed{\lim_{ h \to 0 } \frac{f(x + h) - f(x)}{h}} $$

This just means that $h$ is extremely close to $0$, but is not equal to $0$.

This is the formal definition of a derivative. By plugging in an equation, we can get another equation that gives us the instantaneous slope at any $x$ value.

For example, for $f(x) = x^2$:

$$ \begin{align} &\lim_{ h \to 0 } \frac{(x+h)^2-x^2}{h} \\ =&\lim_{ h \to 0 } \frac{x^2+2xh+h^2-x^2}{h} \\ =&\lim_{ h \to 0 } \frac{2xh-h^2}{h} \\ =&\lim_{ h \to 0 } \frac{2xh}{h} - \frac{h^2}{h} \\ =&\lim_{ h \to 0 } 2x-h \\ =&\ \boxed{2x} \end{align} $$

When we plug in an $x$ value of 2, we get $2(2)=4$. The slope of $f(x)=x^2$ at $x=2$ is $4$. When we plug in an $x$ value of 10, we get $2(10)=20$. The slope of $f(x)=x^2$ at $x=10$ is $20$. And so on. You can see how useful this is for almost every field; Real life almost never follows constant rates of change.

Note that when we take the derivative of a linear function, we get a constant value. This is because the slope of a linear function is always the same:

$$ \begin{align} &\lim_{ h \to 0 } \frac{2(x+h)-2x}{h} \\ =&\lim_{ h \to 0 } \frac{2x+2h-2x}{h} \\ =&\lim_{ h \to 0 } \frac{2h}{h} \\ =&\lim_{ h \to 0 } 2 \\ =&\ \boxed{2} \end{align} $$

Other Notation

You may see a derivative represented as $\Large\frac{ dy }{ dx }$, where $dy$ is an incredibly small change in $y$, (our rise) and $dx$ is an incredibly small change in $x$ (our run).

For example, for $f(x)=y=x^2$

$$ \frac{ dy }{ dx } =\frac{ d }{ dx } x^2=2x $$

and so on.

A second derivative, or a derivative of a derivative looks like:

$$ \frac{ d^{2}y }{ dx^{2} } =\frac{ d^{2} }{ dx^{2} } x^2=\frac{ dy }{ dx } 2x=2 $$

You might also see derivatives as ticks, or primes.

$$ \begin{align} f(x)&=x^2 \\ f'(x)&=2x \end{align} $$

You can keep adding ticks to create second, third, fourth, and so on derivatives:

$$ \begin{align} f(x)&=x^2 \\ f'(x)&=2x \\ f''(x)&=2 \end{align} $$

Special Rules

After finding the derivatives of functions over and over again using the formal definition that we defined above, people began to discover shortcuts. For example,

Using the example of $f(x)=x^3$:

$$ \frac{d}{dx}x^3=3x^{3-1}=3x^2 $$

So the derivative of $x^3$ is $3x^2$

Another rule:

Using the example of $x^2 + 8x + 3$:

$$ \begin{align} &\ \frac{d}{dx}x^2 + 8x + 3 \\ =&\ \frac{d}{dx}x^2+\frac{d}{dx}8x + \frac{d}{dx} 3 \\ =&\ \boxed{2x+8} \end{align} $$

So the derivative of $x^2+8x+3$ is $2x + 8$

There are many many more rules like this. I'm not going to go through them all, but a quick google search can get you more if you're interested.

Note that all of these rules also have mathematical and geometric proofs that clearly explain why they work — these don't come from sheer coincidence. I recommend watching 3Blue1Brown's Calculus Series: Essence of Calculus to learn how some of these rules work.